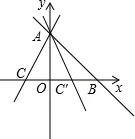
15．已知一次函数y=kx+b与y=2x+2的图象相交于y轴上的点A，且x轴下方的一点P（3，n）在一次函数y=kx+b的图象上，n满足关系式|n-1|=2． （1）求出一次函数y=kx+b的解析式； （2）若上述两个一次函数的图象与x轴的交点分别是点B、C，过点A的直线l，将△ABC的面积分为1：2两部分，试求出直线l的解析式．

15．已知一次函数y=kx+b与y=2x+2的图象相交于y轴上的点A，且x轴下方的一点P（3，n）在一次函数y=kx+b的图象上，n满足关系式|n-1|=2． （1）求出一次函数y=kx+b的解析式； （2）若上述两个一次函数的图象与x轴的交点分别是点B、C，过点A的直线l，将△ABC的面积分为1：2两部分，试求出直线l的解析式．

分析 （1）根据x轴下方点的坐标特征得出n的值，进而得出P点坐标，再利用待定系数法求出一次函数解析式；

（2）根据已知解析式得出B，C点坐标，进而得出直线l的解析式．

解答 解：（1）∵x轴下方的一点P（3，n）在一次函数y=kx+b的图象上，n满足关系式|n-1|=2，

∴n＜0，

∴-n+1=2，

解得：n=-1，

则P（3，-1），

∵一次函数y=kx+b与y=2x+2的图象相交于y轴上的点A，

∴A（0，2），

故$\left\{\begin{array}{l}{3k+b=-1}\\{b=2}\end{array}\right.$，

解得：$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$，

故一次函数y=kx+b的解析式为：y=-x+2；

（2）∵y=-x+2与y=2x+2图象与x轴的交点分别是点B、C，

∴0=-x+2，0=2x+2，

解得：x=2，x=-1，

故B（2，0），C（-1，0），

∵直线l，将△ABC的面积分为1：2两部分，

∴当直线l的解析式为：x=0时，将△ABC的面积分为1：2两部分，

或直线l过（1，0），

则设直线l的解析式为：y=dx+2，

则d+2=0，

解得：d=-2，

故直线l的解析式为：y=-2x+2或直线x=0．

点评 此题主要考查了待定系数法求一次函数解析式，根据题意得出P点坐标是解题关键．